有限状态机简介
一.有限状态机的介绍
首先说说自动机是干什么的。用简单的话来说,有限状态机是一个黑箱,输入是一个合法的字符串(随着你们逐渐深入的学习,这里的“字符串”的概念将会被"Language"替换),输出"Accept"或者"Reject",是不是很像你们的OJ(OJ也是状态机!甚至放开了说,一切程序都是状态机!)而要知道哪些字符串会被"Accept",哪些字符串会被"Reject",我们就需要继续了解状态机的概念。
自动机的工作原理和地图很类似。假设你在你仙林校区,然后你从仙林校区到鼓楼校区,按顺序经过了很多地铁站。每个地铁站都可能有多条换乘路线,而你在所有这些地铁站的选择就构成了一个序列。
例如,你的选择序列是“ 南大仙林校区-> 羊山公园->仙林中心 ->学则路 -> 仙鹤门 -> 金马路 ->马群 -> 钟灵街 -> 孝陵卫 -> 下马坊 -> 苜蓿园 -> 明故宫 -> 西安门 ->大行宫 -> 新街口 -> (转1号线)-> 珠江路 -> 鼓楼”,那你按顺序经过的地铁线路可能是“2号线->1号线"。可以发现,通勤的选择序列不止这一个。同样要去鼓楼校区,你还可以从金马路换乘到4号线,再从4号线到鼓楼站。
而我们如果找到一个选择序列,就可以在地图上比划出这个选择序列能不能去鼓楼校区。比如,如果一个选择序列是“南大仙林校区-> 羊山公园->仙林中心 ->学则路 -> 仙鹤门 -> 金马路 ->马群 -> 钟灵街 -> 孝陵卫 -> 下马坊 -> 苜蓿园 -> 明故宫 -> 西安门 ->大行宫 -> 新街口 -> 上海路->汉中门 -> 莫愁湖 -> 云锦路”,那么它就不会带你去学校,但是仍旧可能是一个可被接受的序列(这里的可接受是任意两个相邻的地点都有地铁能只经过一站而到达),因为目标地点可能不止一个。
也就是说,我们通过这个地图和一组目的地,将信号序列分成了三类,一类是无法识别的信号序列(例如“南大仙林校区-> ???”),一类是能去学校的信号序列,另一类是不能的信号序列。我们将所有合法的信号序列分成了两类,完成了一个判定问题。
既然自动机是一个数学模型,那么显然不可能是一张地图。对地图进行抽象之后,可以简化为一个有向图。因此,自动机的结构就是一张有向图。
而自动机的工作方式和流程图类似,不同的是:自动机的每一个结点都是一个判定结点;自动机的结点只是一个单纯的状态而非任务;自动机的边可以接受多种字符(不局限于 T 或 F)。
例如,完成“判断一个二进制数是不是偶数”的自动机如下:
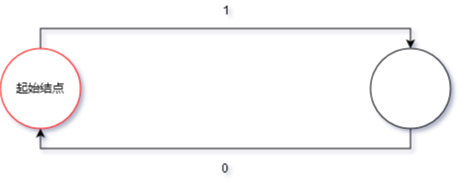
从起始结点开始,从高到低接受这个数的二进制序列,然后看最终停在哪里。如果最终停在红圈结点,则是偶数,否则不是。
如果需要判定一个有限的信号序列和另外一个信号序列的关系(例如另一个信号序列是不是某个信号序列的子序列),那么常用的方法是针对那个有限的信号序列构建一个自动机。这个在学习 KMP 的时候会讲到。(早着呢)
需要注意的是,自动机只是一个 数学模型,而 不是算法,也 不是数据结构。实现同一个自动机的方法有很多种,可能会有不一样的时空复杂度。
二.有限状态机的形式化定义
一个 确定有限状态自动机(DFA) 由以下五部分构成:
- 字符集($\Sigma$),该自动机只能输入这些字符。
- 状态集合($Q$)。如果把一个 DFA 看成一张有向图,那么 DFA 中的状态就相当于图上的顶点。(这里大家没学过图论,但这些基本概念需要大家主动了解,这些概念算是图论里的“常识”了)
- 起始状态($start$),$start \in Q$,是一个特殊的状态。起始状态一般用 $s$表示,为了避免混淆,本文中使用$start$ 。
- 接受状态集合($F$),$F \subseteq Q$,是一组特殊的状态。
- 转移函数($\delta$),$\delta$ 是一个接受两个参数返回一个值的函数,其中第一个参数和返回值都是一个状态,第二个参数是字符集中的一个字符。如果把一个 DFA 看成一张有向图,那么 DFA 中的转移函数就相当于顶点间的边,而每条边上都有一个字符。
DFA 的作用就是识别字符串,一个自动机$A$ ,若它能识别(接受)字符串$S$ ,那么 $A(S)=True$,否则$A(S)=False$ 。
当一个 DFA 读入一个字符串时,从初始状态起按照转移函数一个一个字符地转移。如果读入完一个字符串的所有字符后位于一个接受状态,那么我们称这个 DFA 接受 这个字符串,反之我们称这个 DFA 不接受 这个字符串。
如果一个状态 $v$没有字符$c$ 的转移,那么我们令$\delta(v,c)=null$ ,而$null$只能转移到$null$ ,且$null$不属于接受状态集合。无法转移到任何一个接受状态的状态都可以视作 $null$,或者说, $null$代指所有无法转移到任何一个接受状态的状态。
(注:上一段表示一旦不存在当前状态的某个转移,那么状态机一定会不接受这个字符串)
我们扩展定义转移函数 $\delta$,令其第二个参数可以接收一个字符串:$\delta(v,s)=\delta(\delta(v,s[1]),s[2..|s|])$,扩展后的转移函数就可以表示从一个状态起接收一个字符串后转移到的状态。那么,$A(s)=[\delta(start,s)\in F]$。这里难以理解抽象函数的话,可以当成在字符串中一个个读取字符,然后一步步转移当前状态,最后在最终状态判断是否为接受状态
如,一个接受且仅接受字符串 “a”, “ab”, “aac” 的 DFA:
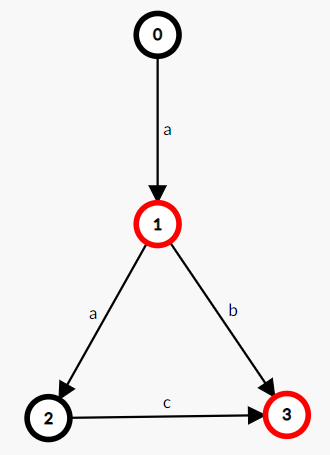
NFA是在DFA的基础上存在某些状态$v$,满足$\delta(v,\epsilon)\neq null$,这里的$\epsilon$表示空字符串,这就导致NFA可能处于多种状态的叠加态中(这是后面将NFA转化成DFA的关键,将当前的多种状态当成一个新状态!这样记原状态数为k种,此时总状态数就会有$2^k$种,但每一次状态转移都是唯一的!),一个NFA的例子如下,我们判断一个字符串是否以"01"结尾,正则表达式表示为"$.*01$“的NFA如下 (S3为接收节点):
graph TD
state1((s1)) -->|0| state2((s2))
state2 -->|e/任意字母|state1
state2 --> |1| state3((s3))
state3 --> |e/任意字母|state1
以上内容节选自OI-Wiki
三.有限状态机的代码实现
1.DFA代码实现
I.非图论建模
非图论建模DFA,主要要确定状态机的各个状态,和状态之间的转移,以上文的只接受"a”,“ab”,“aac"的DFA为例,可以实现一个函数“get_nxt_state()“实现状态的转移。缺点很明显,没有建图的过程,用一个个if判断,代码会冗长不好看
//函数返回值为true表示转移到一个合法状态,函数返回值为false表示转移到一个非法状态
bool get_nxt_state(char ch,int& state){
switch(state){
case 0:{
if(ch=='a')state=1;//合法输入
else return false;//非法输入
return true;
}
case 1:{
...
}
case 2:{
}
}
}
bool dfa(string str){
int status;
for(int i=0;i<str.size();i++){
if(get_nxt_status(str[i],state)==false)
return false;
}
return status在接受状态中;
}
II.图论建模
图论建模DFA,同上,只是在每个状态内部预先处理碰到不同字符后的下一个状态,一种可能的实现方案为
struct Node{
int nxt[128];//不太好的编程习惯
}Nodes[100000];//不太好的编程习惯2,当然这样会超空间
void add(int from,int to,char ch){
Nodes[from].nxt[ch]=to;
}
bool dfa(string str){
int tNode=0;//0是初始节点
//预先设置好每个节点是否是available;
for(int i=0;i<str.size();i++){
tNode=Nodes[tNode].nxt[str[i]];
if(tNode==0x3f3f3f3f)return false;
}
return tNode是一个接受状态;
}
2.NFA代码实现
I.以矩阵和向量的形式建模(NFA 转换成 DFA)
NFA可能在一次状态转移后,可能同时满足多个状态,记NFA的总状态数为k,则可以用一个长度为k的列向量表示当前所处状态,该列向量的第i位表示当前是否可能处于第i种状态,同时可以使用矩阵表示状态之间的转移,转移矩阵需要提前构造。
这个思路中的列向量相当于把所有的状态压缩进一个列向量中,比如共有4个状态,状态1和状态2均有可能,则列向量为{0,1,1,0},列向量共有2^k种不同的可能代表
typedef vector<int>arr;
typedef vector<arr>matrix;
arr operator*(matrix mat,arr vec){
int n=mat.size();
arr ret(n,0);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ret[i]|=mat[i][j]&vec[j];
return ret;
}//矩阵乘列向量
matrix transition_matrix[256];//转移矩阵,其中第i个转移矩阵表示当前遇到的字符为 i时的转移矩阵,其第j行第k列表示可以从第k个状态转移到第j个状态
int state_count;//总的状态数,初始状态为状态0
void dfa_init(string patton){
//TBD 确认状态数
//TBD 构造转移矩阵
}
bool nfa(string str){
arr vec(state_count,0);
vec[0]=1;
for(int i=0;i<str.size();i++){
vec=vec*transition_matrix[str[i]];
}
//最后结果遍历所有vec中为true的位,判断它是否是接受状态
return vec[state_count-1];
}
II.以图论建模,用DFS搜索
用DFS去尝试所有的匹配可能,如果在DFS过程中完成字符串匹配后处于接受状态,则接受这个字符串,否则不接受
vector<vector<int>>graph[10000];//不好的编程风格
//graph[i][j][k]表示当前状态为i,读入的字符为j,能到达的第k个状态的状态号
void add(int from,int to, char ch){
graph[from][ch].push_back(to);
}
bool nfa_dfs(int status,string str,int pl){
if(pl==patton.size())return status为接受状态;
if(graph[status][str[pl]].size()==0)return false;
bool flag=false;
for(int i=0;i<graph[status][str[pl]].size();i++){
flag|=nfa_dfs(graph[status][str[pl]][i],str,pl+1);
if(flag)return true;//剪枝
}
return false;
}
bool nfa(string str){
return nfa_dfs(0,str,0);
}
四.以实际应用为例,进行模型构建和代码实现
1.以匹配合法邮件地址为例
为了方便表示,我们不考虑判断合法域名,以及合法邮件地址,我们给出邮件地址的BNF范式
email address::=\<string '@' domain>
string::=\<word|digit>{word|digit}
domain::=\<string '.' string>
word和digit分别表示单词和数字,定义不给出
例子分析:
我们首先确定状态的个数
- 初始状态
- 位于第一个string的状态
- 位于’@‘的状态
- 位于第二个string的状态
- 位于’.‘的状态
- 位于第三个string的状态
我们注意到,对于本题,合法的邮件地址要求下,只有状态6才是接受状态
接下来分析状态转移
对于状态1,当接收到数字或字母时,会转移到状态2,其他情况均不合法
对于状态2,当接收到数字或字母时,保持当前状态,接收到’@‘时,转移到状态3,其他情况均不合法
对于状态3,当接收到数字或字母时,会转移到状态4,其他情况均不合法
对于状态4,当接收到数字或字母时,保持当前状态,接收到’.‘时,转移到状态5,其他情况均不合法
对于状态5,当接收到数字或字母时,会转移到状态6,其他情况均不合法
对于状态6,当接收到数字或字母时,保持当前状态,其他情况均不合法
代码实现:
接下来有两种代码实现方式,头文件在此均忽略不计
//方案1,状态转移
bool isdigit(char ch){
return '0'<=ch&&ch<='9';
}
bool isletter(char ch){
return ('a'<=ch&&ch<='z')||('A'<=ch&&ch<='Z');
//注意不要写成 'a'<=ch<='z'这样的情况,否则相当于('a'<=ch)<='z'
}
//此函数是表示给出当前状态和当前读入的字符,判断是否存在合法转移,以及如果合法,跳转到下一个状态
//对于函数的参数的"&"符号,可以了解一下实参和形参,以及函数的副作用
//注意这种写法较为冗长,可以建立一个accept的列表
bool get_next_state(char ch,int& state){
switch(state){
case '1':{
if(isdigit(ch)||isletter(ch)){
state=2;
return true;
}
return false;
break;//这里的break不需要,仅仅是为了提醒大家switch里记得不要漏掉break语句
}
case '2':{
if(isdigit(ch)||isletter(ch)){
state=2;
return true;
}
else if(ch=='@'){
state=3;
return true;
}
return false;
break;
}
case '3':{
if(isdigit(ch)||isletter(ch)){
state=4;
return true;
}
return false;
break;
}
case '4':{
if(isdigit(ch)||isletter(ch)){
state=4;
return true;
}
else if(ch=='.'){
state=5;
return true;
}
return false;
break;
}
case '5':{
if(isdigit(ch)||isletter(ch)){
state=6;
return true;
}
return false;
break;
}
case '6':{
if(isdigit(ch)||isletter(ch)){
state=6;
return true;
}
return false;
break;
}
}
}
//另一种get_next_state的实现如下
bool get_next_state(char ch,int& state){
static bool init=false;
struct table{
string str;
int next_state;
};
static vector<table>nextstate[7];
if(!init){
//将合法状态加入表格中,这个合法状态字符串常量可以用一个const string 表示,下文用String表示字符串常量"abcdefghijklmnopqrstuvwxyz0123456789"
table[1].push_back((table){String,2});
table[2].push_back((table){String,2});
table[3].push_back((table){String,4});
table[4].push_back((table){String,4});
table[5].push_back((table){String,6});
table[6].push_back((table){String,6});
table[2].push_back((table){"@",3});
table[4].push_back((table){".",5});
init=true;
//当然这个步骤可以在函数外部完成
}
for(int i=0;i<nextstate[state].size();i++){
//遍历合法状态
string availstr=nextstate[state][i].str;
for(int j=0;j<availstr.size();j++){
if(ch==availstr[j]){
state=nextstate[state][i].next_state;
return true;
}
}
}
return false;
}
bool solve(){
string str;//推荐使用string存放字符串数据
cin>>str;
int state=1;
for(int i=0;i<str.size();i++){
if(!get_next_state(str[i],state)){
return false;//如果转移不合法,则返回false
}
}
return state==6;//只有状态6是接受状态
}
int main(){
int t=1;
while(t--)solve();
}
如果大家注意到的话,第二种方式可以当做”图“来理解,”图“在计算机中只是一种模型,并不一定只有了解”图“的知识,才能写出来含有”图“思想的题目,我这里避免了使用传统建图的方式,不过这里的状态转移表的思想和”图"类似
其他例题:
https://leetcode.cn/problems/valid-number/ (这玩意居然还标了困难…是我大意了,以为是个比较简单的题目…不过LeetCode上的困难题大家大二以后都是随便手撕的(误) 但总的来说,LeetCode是一个适合新手练习的网站,LeetCode中,所有错误都会把错误样例给你,便于调试和debug)
2.更简易正则表达式
为了给大家一个NFA建模的例子,同时保证不直接提供OJ代码,我这里将以一个更简易版的正则表达式的判别
这里的正则表达式只包含26个小写字母和”*“符号,其含义和OJ中正则表达式的含义相同
例子分析
首先要对正则表达式进行语法分析,得到该正则表达式对应的所有状态
对于正则表达式”a*a*“来说,用它去匹配"aa”,可能有多重匹配的结果,比如第一个’a’匹配了两次,第二个’a’匹配了零次,和第一个’a’匹配一次,第二个’a’匹配一次,和第一个’a’匹配零次,第二个’a’匹配两次。因此同一个字符串,可能在正则表达式中有多种对应的匹配**(思考一下如何计算到底有多少种可能的匹配方式呢)**。因此我们可以将正则表达式建模成NFA
以"a*aba*“为正则表达式举例,连同初始状态,它一共有以下四个状态
- 初始状态
- 正在匹配第一个"a*”
- 正在匹配"b”
- 正在匹配第二个"a*"
注意:由于正则表达式的NFA特性,导致初始状态时,既可以处在状态1,也可以处在状态2(当前匹配了0次’a’,为合法的匹配)
代码实现:
我这里将给出上文提到的两种实现方式去解决该问题,当然,对于本题,动态规划也是一个可行的算法,这里不多赘述
//NFA转化成DFA去做
typedef vector<int> arr;
typedef vector<arr> matrix;
arr operator*(matrix mat,arr vec){
assert(mat.size()>0&&vec.size()>0&&mat[0].size()==vec.size());//矩阵运算的前提
int n=mat.size(),m=vec.size();
arr ret(n,0);
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
ret[i]|=mat[i][j]&vec[j];//0-1矩阵计算
}
}
return ret;
}
struct _state{
char ch=0;//这里因为没有出现一个state里允许多字符的'[]'和'.'出现,于是用char表示当前状态允许的字符
int type=0;//当前state的修饰符状态,0表示无修饰符,1表示用'*'修饰,这里建议了解一些enum,在完成较大工程时适合使用
};
//正则表达式的parse过程,将正则表达式标记成多个状态
vector<_state> parse(string regex){
vector<_state>states;
for(int i=0;i<regex.size();i++){
_state state;
state.ch=regex[i];
state.type=0;
if(i+1<regex.size()&®ex[i+1]=='*'){
i++;
state.type=1;
}
states.push_back(state);
}
return states;
}
bool solve(){
string regex;//正则表达式
string str;//被匹配的字符串
cin>>regex>>str;
vector<_state>states=parse(regex);
int state_count=states.size()+1;//总共的状态数
//初始化合法状态
arr state(state_count,0);//表示当前状态
state[0]=1;
for(int i=0;i<states.size();i++){
if(states[i].type==1){
state[i+1]=1;
}
else break;
}
//接下来构建转移矩阵的部分,每一个字母有一个独特的转移矩阵,转移矩阵含义照上文解读
vector<matrix>trans_matrix(26,matrix(state_count,arr(state_count,0)));
int lastavail=0;//这里表示连续的'*'的开始位
for(int i=0;i<states.size();i++){
int index=states[i].ch-'a';
int type=states[i].type;
if(type==1){
//如果当前是"*"的话,那么对于之前的状态,只要他们能到达上一个状态,都能实现转移到当前状态(epsilon边)
for(int j=0;j<=i;j++){
for(int k=0;k<26;k++)trans_matrix[k][i+1][j]=trans_matrix[k][i][j];
}
trans_matrix[index][i+1][i+1]=1;
trans_matrix[index][i+1][i]=1;//这个是多余的(因为能到达i的话,一定能到达状态i+1,但是是可行的)
}
else{
trans_matrix[index][i+1][i]=1;
//否则只能实现从i到i+1的转移
}
}
//不断转移计算
for(int i=0;i<str.size();i++){
state=trans_matrix[str[i]-'a']*state;
}
return state[state_count-1];//正则表达式的支持状态只有末状态.
}
int main(){
int t=1;
while(t--){
solve();
}
}
//DFS去做
struct _state{
char ch=0;//这里因为没有出现一个state里允许多字符的'[]'和'.'出现,于是用char表示当前状态允许的字符
int type=0;//当前state的修饰符状态,0表示无修饰符,1表示用'*'修饰,这里建议了解一些enum,在完成较大工程时适合使用
};
//正则表达式的parse过程,将正则表达式标记成多个状态
vector<_state> parse(string regex){
vector<_state>states;
for(int i=0;i<regex.size();i++){
_state state;
state.ch=regex[i];
state.type=0;
if(i+1<regex.size()&®ex[i+1]=='*'){
i++;
state.type=1;
}
states.push_back(state);
}
return state;
}
vector<_state>states;
int lastavail;//详情见dfs
bool dfs(string str,int index, int state){
if(index==str.size())return state==states.size();
//首先判断当前state可以转移的state
vector<int>availstate;
//注意当前的state下标在states数组里应该是states[state-1]
if(state>0&&states[state-1].type==1&&str[index]==states[state-1].ch)availstate.push_back(state);
//可以贪心,对于所有的可到达的"*"标志,只要进入最小下标的可到达的"*"标记位置即可,这是一种剪枝策略,这里不使用该剪枝策略,不用剪枝策略的话,复杂度最高可以达到2^n
//(为什么可以这样贪心,请自己理解,不懂可以问助教)
for(int i=state;i<states.size();i++){
if(states[i].type!=1){
if(states[i].ch==str[index])availstate.push_back(i+1);
break;
//这里碰到一次type==0的情况后,仍然可以转移到它后面的type==1的情况,但是那样是无意义的,于是这里我写了一个lastavail的标志,表示可以通过epsilon转移到最后一个状态的最小state
}
else{
if(states[i].ch==str[index])availstate.push_back(i+1);
}
}
for(int i=0;i<availstate.size();i++){
if(dfs(str,index+1,availstate[i]))return true;//这里也是简单的剪枝,不剪枝的写法如下
}
/*
不剪枝的写法
bool flag=false;
for(int i=0;i<availstate.size();i++){
flag|=dfs(str,index+1,availstate[i]);
}
return flag;
*/
return false;
}
bool solve(){
string regex;
string str;
cin>>regex>>str;
states=parse(regex);
vector<int>initialstate;
initialstate.push_back(0);
lastavail = states.size();
for (int i = states.size()-1; i >= 0; i--) {
if (states[i].type == 1)lastavail = i;
else break;
}
return dfs(str,0,0);
}
动态规划解法:
自行了解一下 ( https://leetcode.cn/problems/regular-expression-matching/)