【问题求解II-HW3.A】签到题

遇到复杂的表达式不要慌，应当仔细观察它的性质。我们很容易发现该表达式的一个特点：除了 $\min$ 这个操作，其他的三项都是随着区间的扩大而增加的。换句话说，如果没有 $\min$ 这一项，这题的答案就是整个数列。

接下来我们考虑如何对付这个棘手的 $\min$。$\min$ 的一大特点在于它是有限的——任何一个区间的 $\min$ 一定是原数列中的一个数，因此所有可能的 $\min$ 最多只有 $n$ 种。如果我们把所有的区间按照 $\min$ 的位置归类，那么根据之前的结论，享有同一个 $\min$ 的区间集合中，只有最长的那个才可能是答案的候选区间。

到这里，我们的问题转化成了：枚举数列中的每个数 $a_i$ 作为最小值的情况，我们希望找到以此为最小值的最长区间，即从 $a_i$ 出发向左向右扩展，把所有 $\geq a_i$ 的数纳入到区间中，直到碰到边界/比 $a_i$ 小的数。但这件事仍然不容易，如果暴力地向左向右查看，复杂度仍然会达到 $O(n^2)$。

考虑这样一种精巧的做法：我们不按照下标的顺序依次枚举 $a_i$，而是按照 $a_i$ 值从小到大的顺序枚举 $a_i$。这样在枚举到任意 $a_i$ 的时刻整个数列的格局如下：

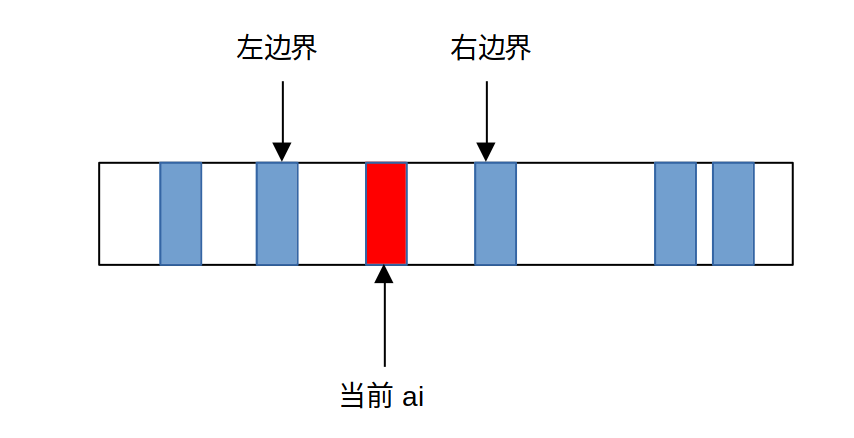
其中蓝色的格子代表已经被枚举过的数，红色的是当前枚举的数。我们发现所有蓝色的数一定比当前数小(小于等于)，所有白色的数一定比当前的数大。因此要寻找“最长区间”，我们只要在“蓝色数”的下标数列中寻找比当前下标小的最大数和比当前下标大的最小数即可。你可以借助 C++ STL 的 set 容器以及 lower_bound 方法来轻松完成这件事，时间复杂度降低到 $O(n\log n)$。

遇到大小相同的数怎么办？

其实不用担心这个问题。你可以按照任意顺序处理大小相同的数，因为先处理的数对应的区间可以包括后处理的数，所以后处理的数被先处理的数“卡住”区间边界也无关紧要了。

或者你也可以采取类似分治的做法，每次找完当前区间的最小值后将区间拆分成左右两个区间分别处理 (因为后续的区间不应该跨越这个最小值)。至于如何寻找一个区间最小值的位置，你可以在维护 ST 表时同时维护最小值位置，具体细节留给大家自己思考。

剩下的最后一件事情是：对于每个最小值，我们找到了它对应的最长区间后，如何求该区间的最大值/同或和/长度。长度是容易的，剩下的两样恰好是 ST 表擅长的内容。你只需要预处理 ST 表即可 $O(1)$ 地查询。整个算法的时间复杂度为 $O(n\log n)$。