问题求解II-HW09 题解
Problem A: 恢复多叉树
- 给定一棵 $n$ 个节点的有根多叉树的前序和后序遍历,求其每一层的最右侧节点的编号。
- $n\leq 50000$。
众所周知,对于二叉树来说知道前序遍历和后序遍历并不能确定唯一的树形态,这是因为有的只有一个子树的节点我们无法确定子树挂在左边还是右边。但事实上,如果只要求确定每一个节点所有孩子的顺序,前后序遍历是足够的。考虑 $solve(l_1, r_1, l_2, r_2)$ 表示分析出前序遍历 $[l_1, r_1]$ 和后序遍历 $[l_2, r_2]$ 对应的子树形态的算法,$solve(1, n, 1, n)$ 即为所求。我们容易发现前序遍历中的 $l_1$ 位置的元素是树根;相对应地,后序遍历中的 $r_2$ 位置的元素也是树根(同一个元素)。进一步,我们可以得出如下的结构:
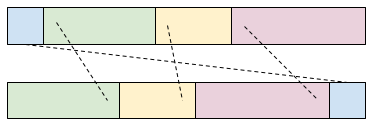
solve 的流程是:我们可以利用前序遍历中每个子树的根到后序遍历中寻找对应的根的位置,从而在后序遍历中确定子树的元素个数,以此类推将所有子树划分好,再递归地对每段子树用 solve 处理。
Problem B: 新马走日
- 给定一个 $n\times m$ 的棋盘和象棋棋子马的初始位置,问经过 $k$ 步到达棋盘上任意点的方案数。
- $n,m\leq 15, k\leq 10^5$。
见 这份题解。