【问题求解II-HW6.C】关押罪犯
题意概述
给定一张 $n$ 个点 $m$ 条边的图 $G=(V, E)$,要求将图上的顶点二染色,使得
$$ \max_{(u, v)\in E, color(u)=color(v)} w(u, v) $$
最小。
基于并查集的思路
这是一道经典的并查集练习题,我们出题的本意是希望大家使用并查集解决。考虑如下最自然的思路:按边权从大到小排序,然后按顺序将边一条一条插入到图中,直到图无法被二染色。你可能会思考为何不能在加边的时候顺便给节点染上色,每次判断新边连接的两个节点是否同色。该做法在连接不同的连通块时会出现问题,例如
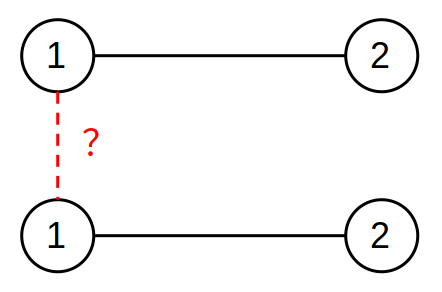
新加入的红色边其实并没有导致问题,我们只要将下面连通块的染色方案换一下就行。但我们每次加边创建出新连通块时无法确定怎么给它染色,因此这条路行不通。我们应该转而去维护点之间的同类关系而不是强行染色,而维护同类关系正是并查集所擅长的。
本题的难点在于:每条边描述的都是“两个点不能属于同一阵营”,如何将其转化为对同类关系的描述?这里有一个非常精妙的技巧。我们创建 $2n$ 个节点,1~n 是原本的节点,n+1~2n 这些节点,$n+i$ 是 $i$ 的“假想敌”。这样如果 $i$ 和 $j$ 之间有边,我们要做的就是在并查集中将 $i$ 和 $n+j$ 合并,$j$ 和 $n+i$ 合并。容易发现“假想敌”的设计非常好地实现了“敌人的敌人是朋友”:如果 $i$ 和 $j$,$k$ 和 $j$ 有边,那么 $i$ 和 $k$ 都会与 $n+j$ 在并查集中合并,从而 $i$ 和 $k$ 属于同一阵营。在每条边 $(i, j)$ 加入之前,我们只需在并查集中查询 $i$ 和 $j$ 的关系,然后按照上面的方法更新关系即可。假设 $n$ 和 $m$ 同阶,理论时间复杂度为 $O(n\alpha(n))$。
基于二分答案的思路
如果你仔细阅读了二分答案章节的讲义,你会发现该问题满足二分答案问题的所有“套路”,尤其是最关键的一点:这是一个最小化最大值的问题。因此我们只需二分答案 $mid$,然后关注由原图中边权大于 $mid$ 的边构成的子图。我们要保证这些边不会落到同一个颜色中,所以要判断该图是否可以二染色。你可以参考 I-Final-C,用一遍搜索完成可二染色判断。假设 $n$ 和 $m$ 同阶,则时间复杂度为 $O(n\log n)$。